Accurate quantum chemistry in the condensed phase.


Developing practical new theoretical models for describing non-covalent interactions and predicting the structures and properties of molecular crystals.

We seek to predict the properties of chemical systems from first principles using quantum chemistry. Quantum chemistry has proved extraordinarily successful in describing gas-phase chemistry. However, many important questions in chemistry today lie in the condensed phases, for which quantum chemistry is much less mature. A major goal of our research is to develop new strategies for modeling intermolecular interactions accurately using currently available computer power. The following sections highlight some of our recent research in the following areas:


Accurate Molecular Crystal Modeling

Molecular Crystal Structure Prediction: Crystal structure prediction exemplifies the challenges faced in modeling the condensed phase. Crystal packing affects the solubility and bioavailability of pharmaceuticals, the efficiency of organic semiconductor materials, and even the taste of chocolate. Drugs such as Ritonavir (for HIV) and Rotigotine (for Parkinson's disease) have been recalled due to the occurrence of insoluble packing motifs ("polymorphs") in the commercial formulations.

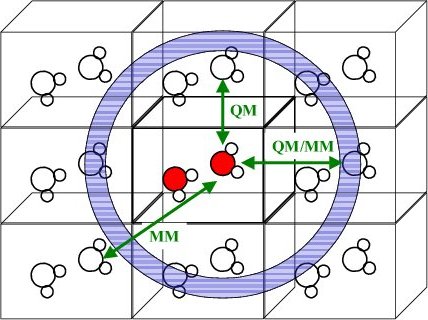
Theory can help by predicting which crystal polymorphs are thermodynamically viable, providing insight into what governs the crystal packing of a given molecule, or even guiding crystal engineering. This requires very accurate energy and structure predictions which often lie beyond what one can obtain with conventional force field or density functional theory (DFT) approaches. We have developed the hybrid many-body interaction model to make it feasible to apply higher-accuracy quantum chemistry techniques to these problems.

Figure 1: Hybrid Many-Body Interaction model for crystals Figure 2: Benzene crystal

The Hybrid Many-Body Interaction (HMBI) Approach: We have developed a hybrid quantum-classical fragment-based QM/MM method for treating molecular liquids and crystals. This fragment model partitions the system into individual molecules, and the important intramolecular and short-range pairwise intermolecular interactions are treated quantum mechanically, while the less important and computationally expensive long-range and many-body interactions are treated classically.

This model exhibits a number of appealing features. First, it very computationally affordable. The computational cost grows linearly with the number of molecules in the unit cell, and we have already studied crystals with more than 160 atoms in the unit cell. Second, the fragment approach enables us to apply very high-level electronic structure methods to obtain an accurate description of intermolecular interactions. Third, by parameterizing the classical polarizable force field terms on the fly using distributed multipole moments, polarizabilities, and dispersion coefficients calculated from density functional theory, the model can predict crystal lattice energies to within a few kJ/mol and crystal structures to within 2-3% of experiment. On-going work seeks to tie these predictions more closely to experiment by developing methods for computing experimentally observable thermochemical and spectroscopic properties.

For more information, see for example:

Recent applications of the HMBI method to polymorphic molecular crystals:

  • Polymorphism in aspirin: A second form of this important pharmaceutical was discovered in 2005. It turns out that both forms I and II exhibit very similar crystal packing (they differ primarily in the interlayer hydrogen bonding), and that the two grow together readily. Our calculations on aspirin found that the two polymorphs are indeed virtually degenerate, and we demonstrated that this degeneracy arises "accidentally" through a competition between adopting a slightly more favorable intramolecular geometry (form I) and forming a cooperative intermolecular hydrogen bond network (form II).
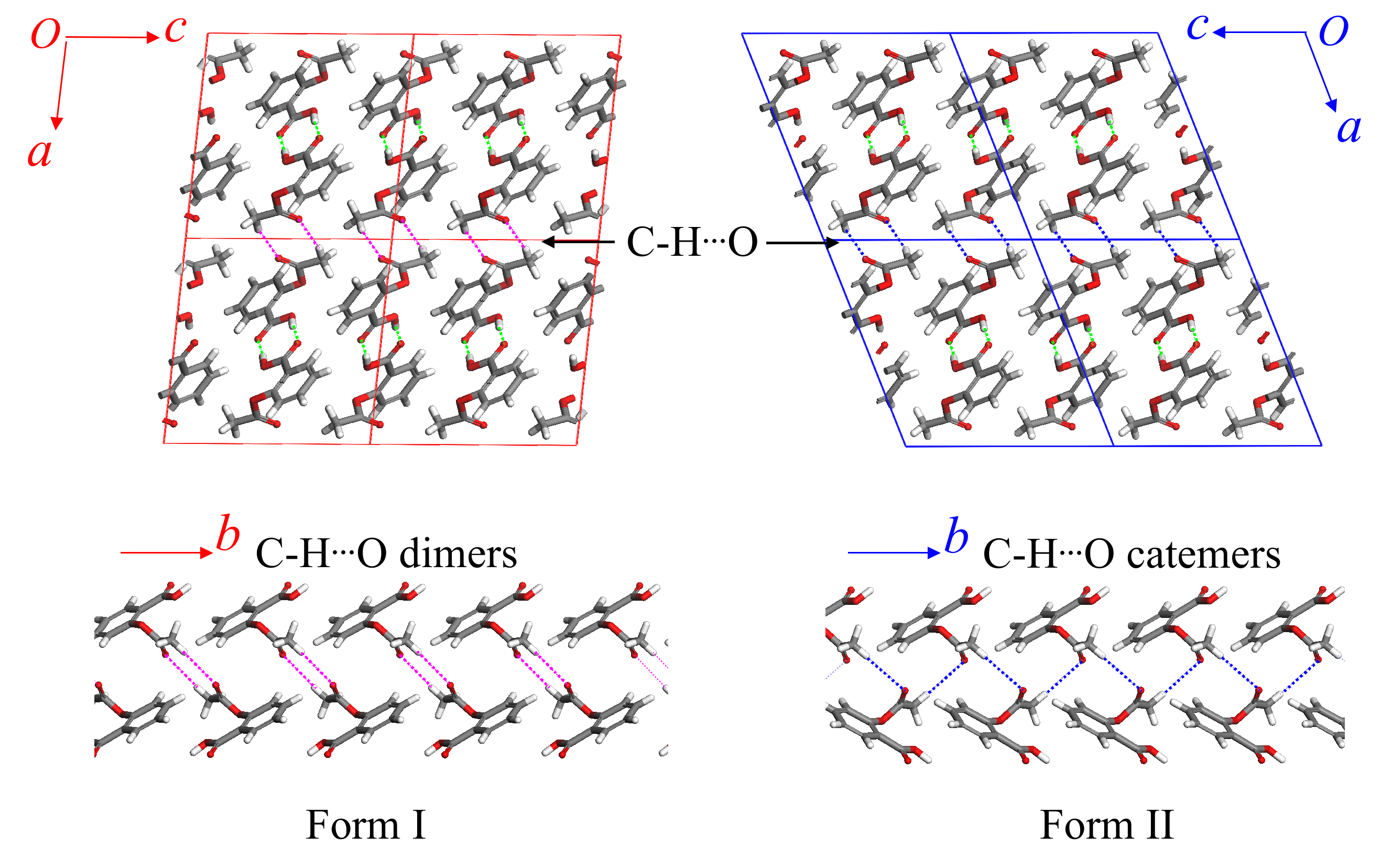
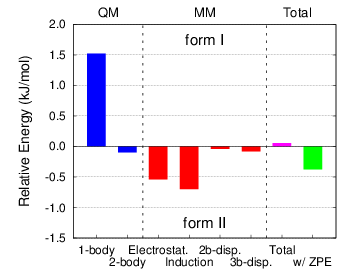
    Figure 3: The two aspirin polymorphs have nearly identical stabilities. Form I adopts a slightly more favorable intramolecular conformation, while the catemeric hydrogen bonding in form II gives it slightly more favorable intermolecular interactions.

    See "Accidental degeneracy in crystalline aspirin: New insights from high-level ab initio calculations." Cryst. Growth. Des. 12, 2169-2172 (2012).

  • Proton-ordering in Ice XV: This newest phase of ice was discovered in 2009, and the proton-ordering inferred from the experiments differed from what had been predicted by several earlier DFT studies. Our MP2 and CCSD(T) calculations, however, confirmed that the experimental structure is the most stable one. We found that the proton-ordering results from a competitition between adopting stronger nearest-neighbor hydrogen bonds versus forming a network with strong, many-body polarization effects. It turns out that the structure with the strongest nearest-neighbor hydrogen bonds is only the second most stable structure. The experimental structure sacrifices nearest-neighbor hydrogen bonding strength in order to maximize the lattice polarization.
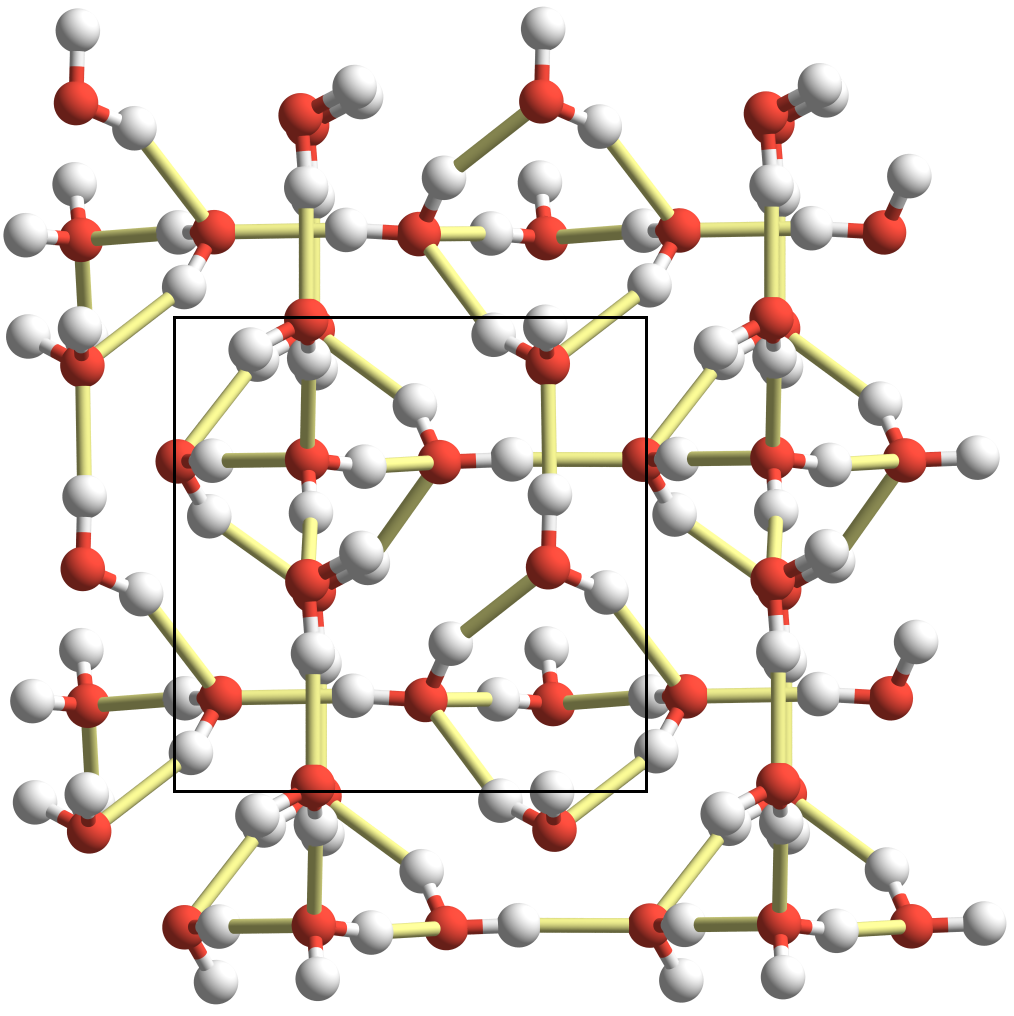
    Figure 4: The experimental proton-ordering of ice XV forms slightly weaker nearest-neighbor hydrogen bonds in order to maximize the polarity/cooperative hydrogen bonding in each hydrogen bond network. Figure 5: Earlier studies incorrectly predicted this proton ordering to be the most stable. It exhibits the strongest nearest-neighbor hydrogen bonds, but it turns out to be slightly less stable overall than the structure at left.

    See "What Governs the Proton-Ordering in Ice XV?" J. Phys. Chem. Lett. 4 , 3165-3169 (2013).

  • Oxalyl dihydrazide: This species has five experimentally known polymorphs which differ in their degree of inter- vs. intramolecular hydrogen bonding. Obtaining reliable predictions for the polymorph ordering has proved challenging. We found that accurate electronic structure treatments and large basis sets were needed to converge the relative energy predictions. In addition, 3-body dispersion had a significant effect on the polymorph energetics. This system highlights the challenge in making robust molecular crystal predictions and the value of being able to apply high-level electronic structure methods with a fragment-based approach.
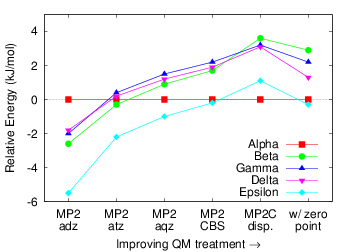
    Figure 6: The relative polymorph ordering of oxalyl dihydrazide converges slowly with respect to the electronic structure treatment. Figure 7: Three-body dispersion plays an important role in determining the relative polymorph stabilities due primarily to the differences in crystal packing density among the polymorphs.

    See "Crystal polymorphism in oxalyl dihydrazide: Is empirical DFT-D accurate enough?" J. Chem. Theory Comput. 8, 2698-2705 (2012).

2) Fast and Accurate Description of Intermolecular Interactions

Obtaining accurate intermolecular interactions at low cost is critical to modeling molecular crystals and many other problems in chemistry. The dispersion-corrected MP2C method of Pitonak and Hesselmann [J. Chem. Theory Comput. 6, 168-178 (2010)] provides near coupled-cluster accuracy at lower cost. Still, evaluating the dispersion correction requires non-trivial computational effort. Normally the monomer density-density response functions needed for the dispersion correction are calculated in a so-called dimer-centered (DC) basis set (i.e. placing basis functions on the "ghost" monomer). However, we have shown that a smaller monomer-centered (MC) basis can be used in this context with almost no loss in accuracy. In molecular crystals, this allows for 100-fold speed-ups for the calculation of the dispersion correction, making it essentially "free" compared to the underlying MP2 calculation. Further efforts for obtaining high-accuracy intermolecular interactions are currently underway.

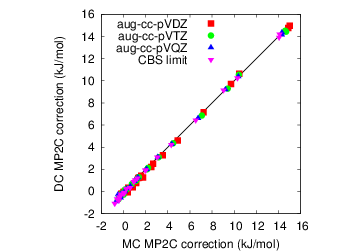Figure 8: Switching to a monomer-centered (MC) basis instead of a dimer-centered (DC) one provides substantial speed-ups in MP2C without compromising the accuracy.

See "Accelerating MP2C dispersion corrections for dimers and molecular crystals." J. Chem. Phys. 138, 224112 (2013).